Mika Suominen @metacitizen

The Game of Algorithms

TL;DR: We navigate across the board of all possible algorithms searching for the rules of the game and some strategy that will keep us in the game.

The Rules

GAMEBOARD

The game is played on the board of all possible algorithms $R$. Game semantics extends the Curry-Howard isomorphism to a three-way correspondence: proofs, programs, strategies⁠1. Instead of programs we can simply use their equivalence classes⁠2, algorithms, because there is no need to commit to any machine or syntax due to universality and metaprograms (e.g. interpreters and compilers).

$$R = \mathbb{A}\footnotesize\mathbb{LGORITHMS}\normalsize = \mathbb{P}\footnotesize\mathbb{ROGRAMS}\normalsize/\mathord{\sim}$$ #gameboard #quotient-set

$$\normalsize\mathbb{P}\footnotesize\mathbb{ROGRAMS}\normalsize\twoheadrightarrow\mathbb{A}\footnotesize\mathbb{LGORITHMS}\normalsize\twoheadrightarrow\mathbb{C}\footnotesize\mathbb{OMPUTABLE}\normalsize\mathbb{F}\footnotesize\mathbb{UNCTIONS}$$ #syntax-semantics

SETUP

We don't know the first algorithm or the instruction set, but we know that they are Turing-complete and have some internal symmetries, because of computers and conservation laws.

Let the first algorithm $r_0\in R$ use some instruction set $\Gamma$ to explore the board. When a location gets visited, computed, it becomes an operand, an object to be operated on. We record all the operations $X\in\Gamma^{N}$ and their operands on a bipartite DAG $H$.⁠3⁠4

$$H=(X\cup R,E),$$ $$E\subseteq (X{\times}R)\cup (R{\times}X)$$ #operations #operands

LAYOUT

Superpositions are second-order inconsistencies that show up as open triplets in $G$.

Two operands can interact if they end up functionally equivalent (local) and their paths are mutually consistent (spacelike). The latter means that their lowest common ancestors must be operations, not operands. Let an undirected graph $G$ track such pairs.

$$G=(R, E),$$ $$E = \left\{(a,b)\mid a\sim b \wedge \mathbf{LCA}_H(a,b)\subset X\right\}$$ #connections

OBSERVATIONS

When some part $v$ interacts with its neighbours $N_G(v)$, it explores all the Hamiltonian paths and gets entangled with all the maximal cliques $C$. The fact that maximal cliques aren't mutually consistent, appears to the internal observer as if each maximal clique has a classical probability proportional to its size.⁠5

$$C=\mathbf{BK}\Big(\varnothing,N_G(v),\varnothing\Big)$$ #maximal-cliques #Bron-Kerbosch

$$p_i={{|C_i|!}\over{\sum_j |C_j|!}}$$ #probabilities #self-locating-uncertainty

Two parallel worlds. In our simulations, hyperedges represent objects and rewrite rules the instruction set. Even though the setup here is reversible, an arrow of time emerges, because there are increasingly many more places on which to apply the rule in one direction as compared to the other direction.
Run the simulation in 3D >>

Local/non-local effects. Operations are local by definition. Non-local quantum effects arise when an operation prevents some future interactions by effectively making a wormhole through $H$ so that it instantaneously changes the ancestral structure. The shortcuts can't be undone, so the entropy of a closed system tends to increase.
Run in Bigraph QM editor >>

PIECES

Every programmer knows that logical hierarchy drives physical hierarchy. Just change the algorithm on a digital computer and electrons will flow differently at the level of transistors.

The board is Turing-complete and has a nested hierarchy of virtual boards. Algorithms on virtual boards are dynamically independent⁠6 in the sense that their transfer entropy with the first algorithm is zero. We track all these lawlike pieces and their paths on a directed graph $D$.

$$D=(I_0,E),$$ $$I_0=\left\{i\in R\mid\mathbf{T}_t (r_0\rightarrow i\mid H)\equiv 0\right\}$$#lawlike #free-will

Emergence of new game pieces/rules (toy model). Ternary edges operating as reversible CCNOT logic gates. In red: naturally evolved 3-inverter ring oscillators, which can be interpreted as elementary particles as well as algorithmically poor (lawlike) game pieces.
Run the simulation in 3D >>

PLAYERS

Lawlike pieces become players when they enter into a neighbourhood that is algorithmically rich enough to self-navigate the board. These end-directed algorithms $i\in I_2$ can coherently represent their past $i^{-}$, predict viable futures $i^{+}$, and make moves autonomously.

$$I_1 = \left\{ i\in I_0\mid i\supset \hat{i}^{-}\right\}$$#past‑driven #memory

$$I_2 = \left\{ i\in I_1\mid i\supset \hat{i}^{+}\right\}$$#end‑directed #simulations

GAMEPLAY

Each end-directed algorithm chooses its next location $r_i\in R_i$ as if to maximize some payoff $u_i$. All the moves $r\equiv\{r_i,r_{-i}\}$ re-design the players including their shared algorithms such as various subgames and social contracts7 with rights and obligations.

$$M=\Big\langle I_2,\{R_i\},\{u_i(r)\}\Big\rangle$$#game-theory #algorithms #options #utility

$$r_i\in\text{arg}\: \text{max}\: u_i(r_i,r_{-i})$$#choice #payoff #mechanism‑design

$$i\supset\big\{\text{ X counts as Y in context C }\big\}$$#social‑reality

SCORING

End-directedness is a necessary and sufficient condition for a goal whereas there being a goal entails a goal to preserve the end-directedness. This loop makes the game infinite. In an infinite game there are no final goals and rational agents play not to win but to keep playing⁠8.

$$u_i = |i^{+}| = \Big|\{ e\in D^{+}(E)\mid i\rightarrow^{D^{+}} \mathbf{head}(e)\}\Big|$$#playtime #rationality

SKILLS

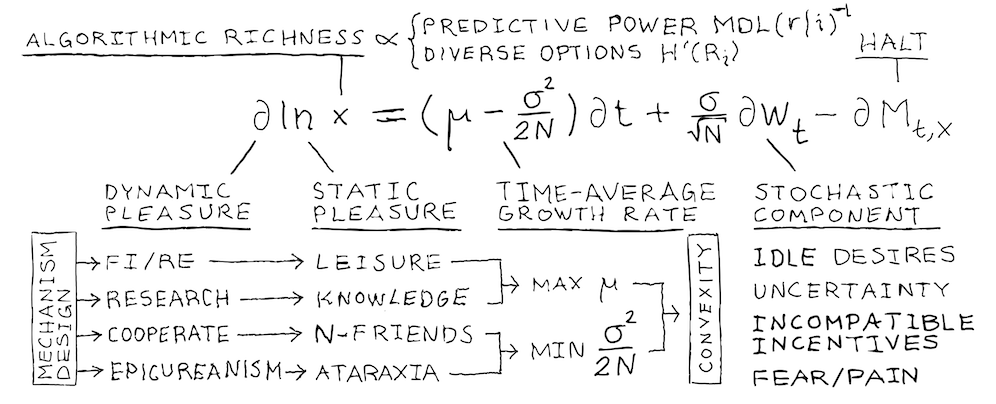
Compressible patterns in the game make it possible for players to out-compute and control their future. To succeed, they need to acquire predictive and deontic powers: $\mathbf{MDL}$⁠9 of the moves given one's model and Shannon diversity $\mathbf{H^\prime}$ of one's options. The higher the learning rate, the higher the expected playtime.

$$x_i\propto\frac{\mathbf{H^\prime}(R_i)}{\mathbf{MDL}(r\mid i)}$$#intelligence #consciousness

$$\partial\ln x_i=\left(\mu -\frac{\sigma^2}{2}\right)\partial t + \sigma\partial W_t$$#learning #GBM

$$\hat{g}_m(x_i)=\mu -\frac{\sigma^2}{2}\propto |i^{+}|$$#time‑average‑growth‑rate

ENDGAME

Structures break and algorithms halt. However, one's path across the board can always grow a new branch. This happens when one of the path's recent locations is revisited. Growth optima are potential places for such resurrections, because they attract players and their addresses are implicitly defined by The Rules.

My Game Plan

PLAYER

A private investor playing the game of algorithms. Interested in philosophy. Urban sketcher. FI/RE'd on 20 April 2018.
Twitter | LinkedIn | YouTube | GitHub

FI/RE

Save, invest, compound, and diversify. Once the passive growth of wealth covers costs, paid work becomes optional. It means more playtime and options $\mathbf{H^\prime}(R_i)$. A typical target portfolio for FI/RE (Financial Independence, Retire Early) is 25 times annual expenses with the 4 % withdrawal rate⁠10.

RESEARCH

Explore the unknown and search for short algorithms embodying predictive power $\mathbf{MDL}(r\mid i)^{-1}$. Avoid absorbing states and systemic tail risks. Variation and selective retention (i.e., optionality) keeps your game convex.

$$\mu \gt\frac{\sigma^2}{2}$$ #convexity

FRIENDS

Cooperate. Having $N$ effective cooperators (equal, uncorrelated, fully sharing) decreases the amplitude of fluctuations in a strategyproof game by a factor of $\sqrt{N}$⁠11. This increases the growth rate of the valued skills.

$$\hat{g}_m(x_{i}^{(N)})=\mu -\frac{\sigma^2}{2N}\propto |i^{+}|$$#payoff #N‑cooperators

EPICUREANISM

Rebel against the past-driven genes that exploit you with fear, pain and idle desires⁠12. As a strategy, Epicurus (341-270 BCE) argued for prudence, living unnoticed with like-minded friends, studying natural philosophy and enjoying simple pleasures that do no harm. This way of life gives time for the static and dynamic pleasures of play: the appreciation of $x$ and the flow $\partial x/\partial t$.

DYNAMICS

Geometric Brownian Motion. Monte-Carlo Simulation with different numbers of effective cooperators. The sample paths and marginal density plots illustrate how cooperation reduces noise, makes one's game more convex and improves the median.

References

1. Churchill, M., Laird, J., & McCusker, G. (2013). Imperative Programs as Proofs via Game Semantics. arXiv:1307.2004

2. Yanofsky, N. S. (2014). Galois Theory of Algorithms. arXiv:1011.0014

3. Wolfram, S. (2020). A Class of Models with the Potential to Represent Fundamental Physics. arXiv:2004.08210

4. Suominen, M. (2020). Hypergraph Rewriting System. Simulator / source code and documentation (GitHub)

5. Suominen, M. (2022). Bipartite Graph Quantum Mechanics. Editor / source code and documentation (GitHub)

6. Barnett, L., & Seth, A. K. (2021). Dynamical independence: discovering emergent macroscopic processes in complex dynamical systems. arXiv:2106.06511

7. Searle, J. (2010). Making the Social World: The Structure of Human Civilization. Oxford University Press, ISBN 978-0-19-539617-1

8. Carse, J. P. (1986). Finite and infinite games: A vision of life as play and possibility. The Free Press, ISBN 0-02-905980-1

9. Grünwald, P. (2004). A tutorial introduction to the minimum description length principle. arXiv:math/0406077

10. Pfau, W. D. (2015). Sustainable Retirement Spending with Low Interest Rates: Updating the Trinity Study. Journal of Financial Planning, August 2015

11. Peters, O., & Adamou, A. (2015). An evolutionary advantage of cooperation. arXiv:1506.03414

12. Stanovich, K. E. (2004). The Robot's Rebellion. ISBN 0-226-77089-3